Nous étudions l’un des modèles les plus simples utilisés dans les épidémies. Nous divisons une population donnée en trois groupes disjoints. La population des individus sensibles est désignée par $S$, la population infectée par $I$, et la population guérie par $R$. Bien entendu, chacune de ces sous-populations est une fonction du temps. Nous faisons les hypothèses suivantes :
- la population totale est constante (pas de naissance ni de décès), de sorte que $\dot{P}=0$, où $P(t)=S(t)+I(t)+R(t)$. Nous désignons par $P_0$ cette constante ;
- le taux de transmission de la maladie est proportionnel au nombre de rencontres entre individus sensibles et infectés. La façon la plus simple de caractériser mathématiquement cette hypothèse est de poser $\dot{S}=-\beta S I$ pour une certaine constante $\beta>0$ qui représente le nombre moyen de contacts par un individu infecté ;
- Les constantes $\nu>0$ et $\mu>0$ représentent respectivement le taux de guérison et le taux de perte d’immunité.
Nous pouvons représenter schématiquement ce modèle par le schéma suivant.
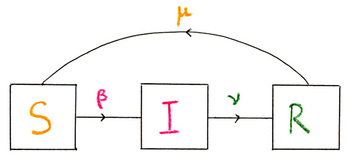
Nous obtenons les équations suivantes :
$$ \begin{cases} \dot{S}= -\beta S I + \mu R \\ \dot{I}= -\beta S I-\nu I\\\ \dot{R}=\nu I -\mu R . \end{cases} $$
À première vue, il s’agit d’un système tridimensionnel. En fait, il se réduit à un système bidimensionnel. En effet, on peut par exemple éliminer $R$ puisque
$$ R=P_0-S-I. $$
Ainsi, si nous déterminons $S(t)$ et $I(t)$, nous déduisons alors $R(t)$ immédiatement. Il en résulte que le modèle initial se résume au système à deux dimensions
$$ \begin{cases} \dot{S}= -\beta S I + \mu (P_0-S-I) \\ \dot{I}=\beta S I-\nu I\\ \end{cases} $$
avec quatre paramètres (positifs) $\beta,\mu,\nu$ et $P_0$.
Nous pouvons vérifier facilement qu’il existe au plus deux points fixes, à savoir $(P_0,0)$ et
$$ (\bar{S},\bar{I})=\left( \frac{\nu}{\beta},\frac{\mu\big(P_0-\frac{\nu}{\beta}\big)}{\nu+\mu}\right). $$
Le premier point fixe correspond clairement à l’absence de toute maladie dans la population. Le second point fixe n’existe que lorsque$$ P_0\geq \frac{\nu}{\beta}. $$
Lorsque $P_0=\nu/\beta$, on a une bifurcation car les deux points fixes se rejoignent à $(P_0,0)$. Le nombre $\nu/\beta$ est appelé le niveau de seuil de la maladie.
On peut aussi trouver les $I$-nullesclines qui sont données par $I=0$ et $S=\nu/\beta$, et la $S$-nulle-cline qui est donnée par le graphe de la fonction.
$$ I(S)=\frac{\mu(P_0-S)}{\beta S+\mu}. $$
Remarquons que seule la région triangulaire du plan $(S,I)$ donnée par $I,S\geq 0$ et $+I\leq P_0$ nous intéresse. En effet, $S$ et $I$ représentent les densités de population, et $P_0=S+I+R\geq S+I$. Par conséquent, le modèle est cohérent si cette région est invariante, dans le sens où si on commence dedans, on y reste pour toujours. Notez que l’axe $I$ n’est pas invariant, alors que sur l’axe $S$, les solutions augmentent jusqu’au point fixe $(P_0,0)$. On peut vérifier que le champ de vecteurs le long de la frontière de cette région triangulaire est soit tangent, soit orienté vers l’intérieur.
Donnons plus de détails. La matrice jacobienne en un point $(S,I)$ se lit comme suit
$$ \begin{pmatrix} -\beta I-\mu & -\beta P_0-\mu \\ \beta I & \beta S-\nu \end{pmatrix}. $$
Lorsque $P_0>\nu/\beta$, le déterminant de la matrice jacobienne au $(P_0,0)$ est égal à $\mu(\nu-\beta P_0)<0$. A l’autre point fixe, on vérifie que le déterminant est égal à $\beta \bar{I}(\beta \bar{S}+\mu)>0$, et la trace est égale à $-\beta\bar{I}-\mu<0$. Par conséquent, $(P_0,0)$ est une selle, alors que $(\bar{S},\bar{I})$ est un puits.
Lorsque $P_0>\nu/\beta$, le seul point fixe est $(P_0,0)$. Le déterminant de la matrice jacobienne en ce point est $>0$, et la trace est $<0$. On a donc un puits.