El estudio gráfico de la ecuación logística que hicimos en el capítulo anterior allana el camino para el caso general. Pues si $\dot{x}=f(x)$, se representa $\dot{x}$ frente a $x$, es decir, la gráfica de $f$. Los puntos de intersección con el eje $x$ son puntos fijos. Entre dos puntos fijos, la gráfica está por encima o por debajo del eje $x$: en el primer caso $\dot{x}>0$, lo que significa que $x(t)$ aumenta y puede representarse dibujando flechas en el eje $x$ que apunten a la derecha; en el segundo caso $\dot{x}<0$, lo que significa que $x(t)$ disminuye y puede representarse dibujando flechas en el eje $x$ que apunten a la izquierda.
Consideremos, por ejemplo, la ecuación
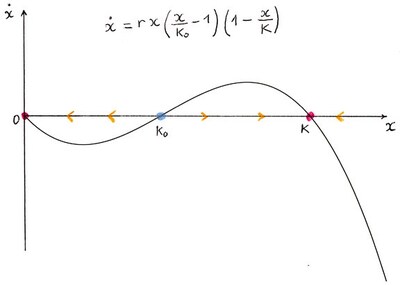
$$ \dot{x}=rx\left(\frac{x}{K_0}-1\right)\left(1-\frac{x}{K}\right) $$
donde $K_0$ y $K$ son parámetros positivos tales que $K_{0}\in (0,K)$. Se trata de una modificación de la ecuación logística en la que existe además un umbral ($K_0$) para el crecimiento. Esto se utiliza para modelar el ‘efecto Allee’ en la dinámica de poblaciones, es decir, la dificultad de encontrar pareja a bajas densidades. Aunque se pueden encontrar soluciones explícitas para esta ecuación, el estudio gráfico proporciona sin esfuerzo las principales características cuantitativas de su comportamiento.
Hasta ahora, hemos dejado pendiente la cuestión de la existencia y unicidad de soluciones del sistema $\dot{x}=f(x)$. Resolvemos esta cuestión en el siguiente apartado y veremos que esto permite responder a preguntas como: ¿cuánto tiempo se necesita para alcanzar un punto fijo?
