L’étude graphique de l’équation logistique que nous avons faite dans un chapitre antérieur ouvre la voie au cas général. En effet, si $\dot{x}=f(x)$, tracez $\dot{x}$ en fonction de $x$, c’est-à-dire le graphe de $f$. Les points d’intersection avec l’axe des $x$ sont les points fixes. Entre deux points fixes, le graphe est soit au-dessus, soit au-dessous de l’axe des $x$ : dans le premier cas, $\dot{x}>0$, ce qui signifie que $t\mapsto x(t)$ est une fonction croissante, ce qui peut être représenté en dessinant des flèches sur l’axe des $x$ qui pointent vers la droite ; dans le second cas, $\dot{x}<0$, ce qui signifie que $t\mapsto x(t)$ décroît et dessine alors des flèches qui pointent vers la gauche.
Considérons par exemple l’équation
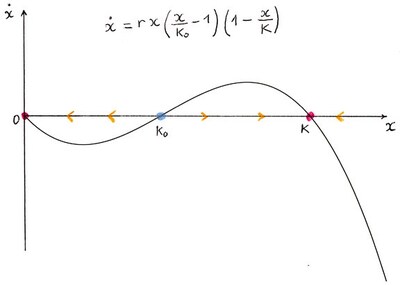
$$ \dot{x}=rx\left(\frac{x}{K_0}-1\right)\left(1-\frac{x}{K}\right) $$
où $K_0$ et $K$ sont des paramètres positifs tels que $K_{0}\in (0,K)$. Il s’agit d’une modification de l’équation logistique dans laquelle il existe en plus un seuil $K_0$ à la croissance. Cela modélise par exemple l’« effet Allee » en dynamique des populations, c’est-à-dire la difficulté de trouver des partenaires quand la densité de la population est faible. Même si on peut trouver des solutions explicites pour cette équation, l’étude graphique fournit sans effort les principales caractéristiques quantitatives de leur comportement.
Jusqu’à présent, nous avons laissé en suspens la question de l’existence et de l’unicité des solutions du système $\dot{x}=f(x)$. Nous réglons cette question dans la prochaine section et nous verrons que cela permet de répondre à des questions comme : combien de temps faut-il pour atteindre un point fixe ?
