Nous voulons cuisiner un exemple simple de cycle limite, une sorte de modèle jouet. Cherchons un système ayant le cercle de rayon un centré à $(0,0)$ comme cycle limite attracteur. L’astuce consiste à penser en termes de coordonnées polaires $(r,\theta)$. La situation la plus simple serait d’avoir des équations non couplées pour les mouvements radiaux et angulaires :
$$ \begin{cases} \dot{r}=f(r)\\ \dot{\theta}=g(\theta). \end{cases} $$
Dans la direction $r$, nous voulons que $f(1)=0$, c’est-à-dire que $r=1$ soit un point fixe. Nous voulons également que $r(t)$ diminue jusqu’à $1$ si $r(0)>1$, et augmente jusqu’à $1$ si $r(0)<1$. Prenons l’équation logistique, c’est-à-dire$$ \dot{r}=r(1-r). $$
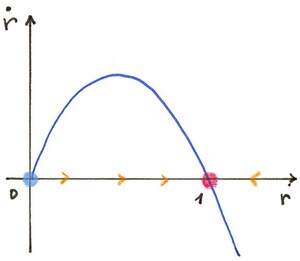
Dans la direction $\theta$, nous pouvons simplement prendre une rotation à vitesse angulaire constante, par exemple $\dot{\theta}=-1$ pour une rotation dans le sens horaire. En combinant les mouvements radiaux et angulaires, on obtient des trajectoires en spirale vers le cercle, des deux côtés.
En revenant aux coordonnées cartésiennes, cela donne des équations beaucoup plus compliquées qui sont couplées :
$$ \begin{cases} \dot{x}= y +x\big(1-\sqrt{x^2+y^2}\big)\\N \dot{y}=-x+ y\big(1-\sqrt{x^2+y^2}\big). \end{cases} $$