Veamos un ejemplo elemental procedente de la mecánica clásica.
El oscilador armónico es el ejemplo más sencillo de una partícula de masa $m$ constreñida a una línea recta, que tomamos como eje $x$, sometida a una fuerza $f(x)$ cuando se encuentra en $x$. Suponer que esta fuerza es independiente de la velocidad $\dot{x}$ equivale a excluir el rozamiento. Según la segunda ley de Newton, tenemos
$$ m \ddot{x}=f(x). $$
En el caso del oscilador armónico, $f(x)=-kx$, donde $k=\text{const.}>0$. El signo menos indica que la fuerza es restauradora. Un ejemplo de oscilador armónico es un muelle de Hooke: $x$ es la desviación de su longitud relajada. Dejando $\omega^2=\frac{k}{m}$ reescribimos la ecuación como$$ \ddot{x}+\omega^2 x =0. $$
(Nótese que $\omega$ tiene la dimensión de una frecuencia, es decir, la inversa de un tiempo).Esto se llama una ecuación diferencial de segundo orden ya que la función desconocida $x(t)$ está definida por una ecuación que implica su segunda derivada. Quizás recuerdes cómo resolver analíticamente esta ecuación en términos de senos y cosenos. Esto se debe a que es una ecuación lineal. Para las ecuaciones no lineales, encontrar una solución analítica está en general fuera de nuestro alcance. Por eso queremos desarrollar métodos para deducir el comportamiento de ecuaciones como ésta sin llegar a resolverla.
Representación del plano de fase.
Para aplicar la misma estrategia que para el modelo de Volterra sobre sardinas y tiburones, tenemos que hacer un paso previo. El estado de nuestro oscilador armónico se caracteriza por dos variables: su posición actual $x$ y su velocidad $\dot{x}$. El truco consiste en reescribir la ecuación $\ddot{x}+\omega^2 x =0$ en términos de $x$ e $y:=\dot{x}$ de la siguiente manera:
$$ \begin{cases} \dot{x}= y\\ \dot{y}=-\omega^2 x. \end{cases} $$
La primera ecuación es sólo la definición de velocidad, y la segunda es la ecuación diferencial original escrita en términos de $y$, ya que $\dot{y}=\ddot{x}$.
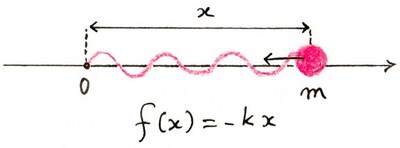
Lo que conseguimos es reinterpretar el movimiento de una masa sobre la recta sometida a una fuerza lineal restauradora como una partícula puntual imaginaria que fluye en el plano $xy$ según el campo vectorial $(y,-\omega^2 x)$. Tratamos la velocidad de la masa de la ecuación original como una segunda dimensión. En particular, podemos ver la aceleración geométricamente, es decir, como el componente $y$ de la posición de la partícula en el plano de fase.
Podemos tener en cuenta que la masa sufre una fuerza de rozamiento proporcional a su velocidad. Esto conduce a la ecuación $\ddot x= -kx -\varepsilon \dot x$, donde $\epsilon>0$ es el coeficiente de rozamiento. En el plano de fase se obtiene
$$ \begin{cases} \dot{x}= y\\ \dot{y}=-\omega^2 x-\epsilon y. \end{cases} $$
Cuando $\epsilon=0$, vemos que, como para el modelo de Volterra, todas las trayectorias en el plano de fase son curvas cerradas, muy probablemente elipses. ¿Qué tiene esto que ver con el problema original? La respuesta es muy sencilla. El punto fijo $(x,y)=(0,0)$ corresponde al equilibrio estático del sistema: la masa está en reposo en su posición de equilibrio y permanecerá allí para siempre. Las trayectorias cerradas corresponden, como es de esperar, a movimientos periódicos, es decir, oscilaciones de la masa. Si sabes o recuerdas algo de física elemental, es fácil demostrar por qué las trayectorias son en realidad elipses dadas por la ecuación $\omega^2 x^2 + y^2=C$, donde $C\geq 0$ es una constante determinada por la posición inicial y la velocidad de la masa: esto equivale a la conservación de la energía. Sin embargo, en cuanto $\epsilon>0$, vemos que las soluciones se dirigen en espiral hacia el origen. La interpretación es sencilla: ahora las trayectorias no se cierran porque la masa pierde un poco de energía en cada instante.
Sistemas lineales bidimensionales.
Terminemos con un comentario matemático. La ecuación
$$ \begin{cases} \dot{x}= y\\ \dot{y}=-\omega^2 x-\epsilon y. \end{cases} $$
es una instancia especial de un sistema lineal bidimensional que es genéricamente de la forma
$$ \begin{cases} \dot{x}= ax+by\\ \dot{y}=cx+dy \end{cases} $$
donde $a,b,c,d$ son parámetros reales. Si utilizamos negrita para denotar los vectores, esto se puede escribir de forma más compacta en forma de matriz como
$$ \dot{\boldsymbol{x}}=A \boldsymbol{x} $$
donde
$$ A=\begin{pmatrix}a & b\\ c & d\end{pmatrix}\quad\text{and}\quad\boldsymbol{x}=\begin{pmatrix}x\\ y\end{pmatrix}. $$
Para el oscilador armónico se tiene
$$ A=\begin{pmatrix}0 & 1\\ -\omega^2 & -\epsilon\end{pmatrix}. $$
Más adelante veremos cómo clasificar todos los retratos de fase de sistemas lineales bidimensionales.
