Hasta ahora hemos estudiado lo más sencillo que puede hacer una solución de una ecuación diferencial: ser atraída o repelida por un punto fijo. Lo siguiente más sencillo que puede hacer es comportarse periódicamente en el tiempo, es decir, trazar una curva cerrada, llamada ciclo. Ya hemos visto ejemplos de soluciones periódicas en la primera parte de este ebook. En particular, hemos visto un ejemplo de ciclo límite estable o atrayente. Corresponde a oscilaciones autosostenidas que son robustas ante pequeñas perturbaciones. Tales ciclos límite aparecen en sistemas físicos, biológicos y químicos. Veremos que estos objetos sólo se dan en sistemas no lineales.
Soluciones periódicas y ciclos
Consideremos un sistema bidimensional
$$ \begin{cases} \dot{x}=f(x,y)\\ \dot{y}=g(x,y) \end{cases} $$
donde $(x,y)\in\mathbb{R}^2$ y $f,g:\mathbb{R}^2\to\mathbb{R}$ son funciones continuamente diferenciables. Decimos que una solución $(x(t),y(t))$ es periódica si existe algún número $T>0$ tal que
$$ x(t)=x(t+T) \quad \text{and}\quad y(t)=y(t+T)\quad\text{for all}\thinspace t. $$
El periodo de esta solución se define al mínimo tal $T$. La trayectoria de una solución periódica es una curva cerrada en el plano $xy$ (ciclo). Nótese que una solución constante (es decir, un punto fijo) no se considera solución periódica.
Remark. Para definir soluciones periódicas, basta con exigir que exista un tiempo $T>0$ tal que $x(0)=x(T)$ y $y(0)=y(T)$. Entonces, por el enunciado sobre unicidad de soluciones de ecuaciones diferenciales, debemos tener $x(t)=x(t+T)$ e $y(t)=y(t+T)$ para todo $t$.
Los ciclos no pueden aislarse para los sistemas lineales.
El ejemplo más simple que hemos conocido es el oscilador armónico descrito por el sistema lineal
$$ \begin{cases} \dot{x}= y \\ \dot{y}=-x. \end{cases} $$
Vemos que ninguno de los ciclos está aislado. Esto es, de hecho, una característica general de los sistemas lineales. En efecto, supongamos que se nos da un sistema lineal $\dot{\boldsymbol{x}}=A\boldsymbol{x}$ tal que existe una solución periódica $\boldsymbol{x}(t)$. Entonces también lo es $c\thinspace\boldsymbol{x}(t)$ para cualquier constante $c\neq 0$, por linealidad. Por tanto, el ciclo asociado a $\boldsymbol{x}(t)$ está rodeado por una familia de ciclos de un parámetro. En particular, la amplitud de una oscilación periódica se establece enteramente por su condición inicial $\boldsymbol{x}_0$. Y cualquier pequeña perturbación de la amplitud persistirá para siempre. Por el contrario, vamos a ver que, en los sistemas no lineales, es posible tener ciclos aislados que controlan el comportamiento de las trayectorias cercanas.
Limit cycles
Supongamos que tenemos un sistema no lineal $\dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x})$ con un ciclo aislado $C$. Por ‘aislado’ queremos decir que, al menos en un ‘anular’ barrio suficientemente pequeño de $C$, no hay otro ciclo. Esperamos que las trayectorias suficientemente cercanas ‘sientan’ su presencia. ¿Qué puede ocurrir? Pues que pueden girar en espiral hacia $C$ o pueden girar en espiral alejándose de $C$. Entonces $C$ se llama ciclo límite.
Es natural decir que $C$ es estable o atrayente si las trayectorias cercanas van en espiral hacia $C$ por ambos lados. Cuando se alejan en espiral de $C$ por ambos lados, decimos que $C$ es inestable o repulsiva. En el caso mixto, decimos que $C$ es semi-estable. Este tercer caso no es genérico.
Construir un ciclo límite desde cero. Queremos cocinar un ejemplo sencillo de un ciclo límite, una especie de modelo de juguete. Busquemos un sistema que tenga el círculo de radio uno centrado en $(0,0)$ como ciclo límite atrayente. El truco es pensar en términos de coordenadas polares $(r,\theta)$. La situación más simple sería tener ecuaciones desacopladas para los movimientos radial y angular:
$$ \begin{cases} \dot{r}=f(r)\\ \dot{\theta}=g(\theta). \end{cases} $$
En la dirección $r$, queremos que $f(1)=0$, es decir $r=1$ sea un punto fijo. También queremos que $r(t)$ disminuya hasta $1$ si $r(0)>1$, y aumente hasta $1$ si $r(0)<1$. Tomemos la ecuación logística, es decir
$$ \dot{r}=r(1-r). $$
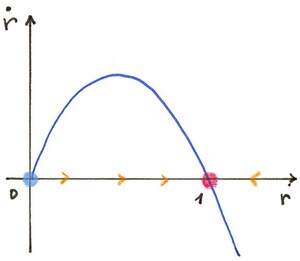
En la dirección $\theta$, podemos simplemente tomar una rotación a velocidad angular constante, por ejemplo $\dot{\theta}=-1$ para una rotación en el sentido de las agujas del reloj. Combinando los movimientos radial y angular, obtenemos trayectorias en espiral hacia el círculo, desde ambos lados.
Volviendo a las coordenadas cartesianas, esto da ecuaciones mucho más complicadas que están acopladas:
$$ \begin{cases} \dot{x}= y +x\big(1-\sqrt{x^2+y^2}\big)\\ \dot{y}=-x+ y\big(1-\sqrt{x^2+y^2}\big). \end{cases} $$
Con la receta anterior, podemos cocinar ejemplos con, digamos, tres ciclos límite:
$$ \begin{cases} \dot{r}= r(1-r)(2-r)(3-r)\\ \dot{\theta}=-1. \end{cases} $$
The circles of radius $1$ and $3$ are stable limit cycles, whereas the circle of radius $2$ is an unstable one.
Así que hemos creado fácilmente ejemplos de ciclos límite a partir de cero. Pero, en la práctica, nos enfrentamos al problema inverso: dado un campo vectorial $\boldsymbol{f}$, ¿cómo sabemos que genera un ciclo límite? ¿Podemos predecir cuántos ciclos límite tendrá? Por supuesto, podemos utilizar experimentos numéricos. Matemáticamente hablando, demostrar la existencia de un ciclo límite puede ser difícil. Predecir cuántos ciclos límite puede haber resulta ser un problema abierto, ¡incluso para campos vectoriales polinómicos!
Demostrar la presencia de un ciclo límite
Aunque los ciclos límite aparecen de forma bastante natural en modelos físicos, biológicos o químicos, no es fácil probar matemáticamente la existencia de un ciclo límite. La principal herramienta para ello es la llamada teoría de Poincaré-Bendixson. Enunciamos deliberadamente el siguiente teorema de forma amigable, y no en su forma más general.
Teorema de Poincaré-Bendixson.Considere un sistema$$ \begin{cases} \dot{x}=f(x,y)\\ \dot{y}=g(x,y) \end{cases} $$
donde $f$ y $g$ tienen derivadas parciales continuas, y tales que existen soluciones para todo $t$. Sea $R$ una región cerrada y acotada del plano $xy$ que no contiene puntos fijos. Supongamos que ninguna solución puede salir de $R$. Entonces el sistema tiene una solución periódica en la región $R$.
Es común llamar a la región $R$ región trampa, ya que, si y cuando cualquier solución entra en $R$, ya no puede salir de ella. Así que, para aplicar el teorema, nuestra tarea es encontrar una región tal que, si viajamos a lo largo de su frontera, siempre seamos empujados dentro de la región. Matemáticamente, esto significa que el campo vectorial apunta hacia dentro a lo largo de la curva que delimita $R$. En general es difícil encontrar una región de atrapamiento. Veremos ejemplos en la continuación.
Una consecuencia del teorema de Poincaré-Bendixson es que si existe una trayectoria cerrada en un sistema bidimensional, entonces debe contener un punto fijo.
Desde un punto de vista intuitivo, el teorema de Poincaré-Bendixson es un resultado bastante plausible. En efecto, toda solución que comienza en $R$ permanece allí para siempre, y no puede aproximarse a un punto fijo. No puede tender al infinito ya que $R$ está acotado, por suposición. Ahora, elija un punto $(x_0,y_0)$ dentro de $R$ y ejecute la solución correspondiente. Si en algún momento $t>0$ tenemos $(x(t),y(t))=(x_0,y_0)$, entonces esto significa que tenemos una solución periódica. Si no existe tal tiempo, hay dos escenarios ya que una trayectoria no puede auto-intersecarse. O bien la solución acaba girando, digamos, en el sentido de las agujas del reloj, o bien tiene que dar un número infinito de vueltas para cambiar el sentido en el que gira. En el primer caso, tiene que ‘apilarse’ en una trayectoria cerrada. En el segundo caso, como la trayectoria no puede cruzarse a sí misma, esto implica que los giros se hacen cada vez más bruscos; a la larga, esto contradice la diferenciabilidad del campo vectorial. Sin embargo, una demostración rigurosa del teorema de Poincaré-Bendixson es bastante larga y requiere toda la fuerza de un teorema de topología de apariencia inocente, a saber, el teorema de la curva de Jordan.
Atención. El teorema de Poincaré-Bendixson no se generaliza a tres o más dimensiones. Veremos más adelante las consecuencias trascendentales de este hecho.
Descartar la presencia de un ciclo límite
A continuación presentamos herramientas que pueden utilizarse para eliminar la posibilidad de tener ciclos.
Teorema de Bendixson.Considere un sistema$$ \begin{cases} \dot{x}=f(x,y)\\ \dot{y}=g(x,y) \end{cases} $$
donde $f$ y $g$ tienen derivadas parciales continuas en algún dominio $D$ simplemente conexo del plano $xy$. (Por ‘simplemente conexo’ queremos decir que el dominio no tiene ‘agujeros’ o porciones disjuntas). Entonces, si la cantidad$$ \frac{\partial f}{\partial x}(x,y)+\frac{\partial g}{\partial y}(x,y) $$
no es idénticamente cero (es decir, no es cero para todo $(x,y)\in D$) y es de un signo en $D$, no hay ciclos dentro de $D$.
Demos la prueba de este (…)
Demos la prueba de este teorema que es por contradicción. Supongamos que tenemos una trayectoria cerrada $C$, con interior $I$, contenida en $D$.
We apply Green’s theorem which says that
$$ \oint_C (f\boldsymbol{i}+g\boldsymbol{j})\cdot \boldsymbol{n}\, \text{d}s \equiv \oint_C f\text{d}y-g\text{d}x = \iint_I \left( \frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}\right) \, \text{d}x\text{d}y $$
donde $\boldsymbol{i}$ (resp. $\boldsymbol{j}$) es el vector unitario en la dirección $x$ (resp. en la dirección $y$), y $\boldsymbol{n}$ es la normal exterior a la curva $C$. Por hipótesis, el integrando del lado derecho es continuo y nunca cero; por lo tanto, es siempre positivo o siempre negativo, y el lado derecho es positivo o negativo.
Por otra parte, el lado izquierdo debe ser cero. Pues como $C$ es una trayectoria cerrada, $C$ es siempre tangente al campo vectorial $f\boldsymbol{i}+g\boldsymbol{j}$. Esto significa que $\boldsymbol{n}$ es siempre perpendicular a $f\boldsymbol{i}+g\boldsymbol{j}$, por lo que el integrando $(f\boldsymbol{i}+g\boldsymbol{j})\cdot \boldsymbol{n}$ es idénticamente cero. Llegamos así a una contradicción, por lo que concluimos que no puede existir ninguna trayectoria cerrada en $D$.
Remark.
La cantidad que aparece en el teorema de Dulac no es otra cosa que la divergencia del campo vectorial. Recordemos nuestra interpretación de una ecuación diferencial como descripción de un flujo de fluido imaginario: el campo vectorial da la velocidad del fluido en cada punto $(x,y)$. Entonces, la divergencia del campo vectorial es la medida en que el flujo se comporta como una fuente o un sumidero en $(x,y)$. Es una medida local de hasta qué punto hay más saliendo de una región infinitesimal del espacio que entrando en ella. Se puede ver que la divergencia del campo vectorial en el punto $(x,y)$ es la traza de la matriz jacobiana en ese punto.
Ejemplo. Consideremos un sistema lineal bidimensional general
$$ \begin{cases} \dot{x}=ax+by\\ \dot{y}= cx+dy \end{cases} $$
donde $a,b,c,d$ son parámetros reales. Aplicando el teorema de Bendixson encontramos que si $a+d\neq 0$ entonces no hay trayectorias cerradas. Si $a+d=0$, este teorema no dice nada. Pero podemos concluir fácilmente utilizando lo que hemos aprendido sobre sistemas lineales. La función característica del sistema es
$$ \lambda^2 -(a+d)\lambda +(ad-bc)=0. $$
Si $a+d=0$ entonces las soluciones tienen signo contrario si $ad-bc<0$ y el origen es una silla. Si $ad-bc>0$ entonces las soluciones son puramente imaginarias y el origen es un centro. En el caso especial $a=d=0$, $b=1$, $c=-1$ obtenemos el oscilador armónico $\dot{x}=y$, $\dot{y}=-x$ para el que ahora que existe un continuo de trayectorias cerradas. En conclusión, el sistema lineal anterior tiene ciclos si, y sólo si, $a+d=0$, $ad-bc>0$.
Por desgracia, el teorema de Bendixson puede fallar incluso para sistemas sencillos. Pero Dulac ha rescatado este teorema haciendo la siguiente observación, sencilla pero profunda: consideremos el sistema
$$ \begin{cases} \dot{x}= \varphi(x,y)\, f(x,y)\\ \dot{y}= \varphi(x,y)\, g(x,y) \end{cases} $$
donde $\varphi$ es una función continuamente diferenciable, de valor real; comparte el mismo retrato de fase que el sistema
$$ \begin{cases} \dot{x}= f(x,y)\\ \dot{y}= g(x,y). \end{cases} $$
Por lo tanto, si podemos refutar la existencia de una trayectoria cerrada para algunos $\varphi$, se puede refutar la existencia de una trayectoria cerrada para el sistema original.
Teorema de Dulac.Consideremos los mismos supuestos que en el teorema de Bendixson. Además, supongamos que se puede encontrar una función continuamente diferenciable $\varphi:\mathbb{R}^2\to\mathbb{R}$ tal que$$ \frac{\partial (\varphi f)}{\partial x}(x,y)+\frac{\partial (\varphi g)}{\partial y}(x,y) $$
no es idénticamente cero (es decir, no es cero para todo $(x,y)\in D$) y es de un signo en $D$, entonces no hay ciclos dentro de $D$.
La función $\varphi$ suele denominarse función de Dulac. Desgraciadamente, no existe ningún algoritmo para encontrar tales funciones. Apliquemos el teorema de Bendixson-Dulac en dos ejemplos estudiados anteriormente para los que observamos la ausencia de ciclos.
Más tiburones y sardinas. Este es el sistema
$$ \begin{cases} \dot{x}= x\, (1-x-y)\\ \dot{y}= \beta\, (x-\alpha)y \end{cases} $$
donde $\alpha,\beta>0$.
Recordemos que estudiamos este sistema en el interior del cuadrante positivo.
Sea
$$ \varphi(x,y)=\frac{1}{xy} $$
which is well-defined for $x,y>0$.Tenemos
$$ \frac{\partial (\varphi f)}{\partial x}(x,y)+\frac{\partial (\varphi g)}{\partial y}(x,y)=-\frac{1}{y}\cdot $$
Esto es estrictamente negativo, por lo tanto no puede haber ciclos en este modelo.
Volvemos a nuestro modelo de dos poblaciones en competencia. Tenemos las ecuaciones
$$ \begin{cases} \dot{x}= x\, (1-x-a_{12}y)\\ \dot{y}= \rho y\, (1-y-a_{21}x) \end{cases} $$
donde $\rho,a_{12},a_{21}>0$. De nuevo, sólo consideramos el primer cuadrante, y utilizamos la misma función de Dulac que antes. Obtenemos
$$ \frac{\partial (\varphi f)}{\partial x}(x,y)+\frac{\partial (\varphi g)}{\partial y}(x,y)=-\left(\frac{1}{y}+\frac{\rho}{x}\right)\cdot $$
Al ser una cantidad estrictamente negativa para todo $x,y>0$, no hay ciclo en este modelo.