Anteriormente dijimos que la mayoría de las ecuaciones diferenciales no pueden resolverse explícitamente. Esto no es del todo cierto: las ecuaciones diferenciales lineales pueden analizarse a fondo. La mayoría de los modelos en física, biología, etc. son ecuaciones diferenciales no lineales, pero las lineales desempeñan un papel importante en la clasificación de sus puntos fijos, como veremos más adelante.
Definición
Un sistema lineal bidimensional es un sistema de la forma
$$ \begin{cases} \dot{x}= ax+by\\ \dot{y}= cx+dy \end{cases} $$
donde $a,b,c,d$ son parámetros. En notación vectorial esto se escribe de forma más compacta en forma matricial como
$$ \dot{\boldsymbol{x}}=A\boldsymbol{x} $$
donde$$ A= \begin{pmatrix} a & b\\ c & d \end{pmatrix} \hspace{0.5cm}\text{and}\hspace{0.5cm} \boldsymbol{x}= \begin{pmatrix} x\\ y \end{pmatrix}\, . $$
Tales sistemas son la versión bidimensional natural de la ecuación escalar $\dot{x}=ax$ que es la primera que apareció en este ebook. Decimos que es lineal porque si $\boldsymbol{x}_1$ y $\boldsymbol{x}_2$ son soluciones, entonces también lo es cualquier combinación lineal $c_1 \boldsymbol{x}_1+ c_2 \boldsymbol{x}_2$. Obsérvese que $\dot{\boldsymbol{x}}=\boldsymbol{0}$ cuando $\boldsymbol{x}=\boldsymbol{0}$, por lo que $\bar{\boldsymbol{x}}=\boldsymbol{0}$ es siempre un punto fijo para cualquier elección de $A$.
Ejemplos
Volver al oscilador armónico.
Ya conocimos un ejemplo de ecuación diferencial lineal bidimensional, a saber, el oscilador armónico. Recordemos que se trata de una partícula de masa $m$ que se mueve sobre el eje $x$ sometida a la fuerza $f(x)=-kx$. Como vimos, la ecuación de movimiento $\ddot x=-kx$ puede representarse como un sistema lineal bidimensional $\dot{\boldsymbol{x}}=A\boldsymbol{x}$ con
$$ A= \begin{pmatrix} 0 & 1\\ -\omega^2 & 0 \end{pmatrix} $$
donde $\omega^2=\frac{k}{m}$. Podemos añadir una fuerza de fricción de la forma $-\epsilon \dot{x}$, donde $\epsilon>0$, lo que da un sistema lineal bidimensional con
$$ A= \begin{pmatrix} 0 & 1\\ -\omega^2 & -\epsilon \end{pmatrix}. $$
Vemos que, cuando $\epsilon=0$, todas las trayectorias son cerradas y rodean el origen (el único punto fijo) que se llama centro. Cuando $\epsilon>0$, las trayectorias ya no son cerradas: las soluciones van en espiral hacia el origen.
Teoría de los circuitos.
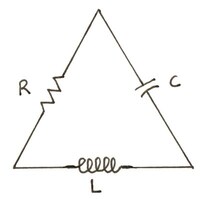
Nuestro siguiente ejemplo procede de la teoría de circuitos, más concretamente de un circuito RLC en serie, donde $R$ significa resistencia, $L$ inductor y $C$ condensador. En este modelo, la resistencia es la única responsable de la disipación de energía, mientras que el inductor y el condensador se idealizan como capaces de almacenar energía sin disiparla.
Suponiendo que el circuito tiene una fuente de alimentación que muestra una tensión constante en el tiempo, podemos aplicar la ley de la corriente de Kirchhoff, la ley de Faraday y la ley de Ohm para obtener la ecuación diferencial de segundo orden
$$ L \ddot{I}+R\dot{I}+\frac{I}{C}=0 $$
donde $I(t)$ es la corriente en el circuito y $L,C>0$ y $R\geq 0$ son parámetros. La ley de Ohm dice que la tensión a través de la resistencia es proporcional a la corriente, siendo la constante de proporcionalidad $R$. Esta relación hace que el sistema sea lineal. Muchas resistencias cumplen la ley de Ohm. (Obsérvese que cuando $R=0$ obtenemos una ecuación que es formalmente la misma que la del oscilador armónico). Podemos reescribir la ecuación como una ecuación diferencial lineal bidimensional estableciendo $x=I$ y $y=\dot{x}$. Esto da
$$ \begin{cases} \dot{x}= y\\ \dot{y}= - \frac{1}{L C}\thinspace x-\frac{R}{L} y \end{cases} $$
thus$$ A= \begin{pmatrix} 0 & 1\\ - \frac{1}{L C} & -\frac{R}{L} \end{pmatrix}. $$
Por cierto, observamos que el sistema obtenido para el circuito RLC tiene exactamente la misma forma que el que describe un oscilador armónico amortiguado si identificamos $\frac{1}{L C}$ con $\omega^2$ y $\frac{R}{L}$ con $\epsilon$. En efecto, $R=0$ corresponde a un circuito ideal en el que no habría disipación de energía por efecto Joule.
Un ejemplo abstracto.
Consideremos ahora el sistema lineal
$$ \begin{cases} \dot{x}= a x\\ \dot{y}= -y \end{cases} $$
donde $a\in\mathbb{R}$ es un parámetro. En notación vectorial, esto significa que $\dot{\boldsymbol{x}}=A\boldsymbol{x}$ con
$$ A= \begin{pmatrix} a & 0\\ 0 & -1 \end{pmatrix}. $$
Las dos ecuaciones están desacopladas en el sentido de que no hay $x$ en la ecuación $y$ y viceversa. Esto implica que cada ecuación puede resolverse por separado. Obtenemos fácilmente
$$ x(t)=x_0\ e^{at},\thinspace y(t)=y_0\ e^{-t}. $$
La geometría de las trayectorias en la vecindad del origen, que es un punto fijo para cualquier valor de $a$, puede explorarse con el siguiente experimento digital interactivo.
Comentemos lo que observamos.
Por supuesto, sabemos que $y(t)$ decrece exponencialmente con $t$ sea cual sea el valor de $a$. Cuando $a<0$, $x(t)$ también decrece exponencialmente y, por tanto, todas las trayectorias se aproximan al origen como $t\to+\infty$. Sin embargo, la dirección de aproximación depende del tamaño de $a$ comparado con $-1$.
Cuando $a<-1$, $x(t)$ decae más rápidamente que $y(t)$. Las soluciones se aproximan al origen tangente a la dirección más lenta, es decir, la dirección $y$. El punto fijo $\bar{\boldsymbol{x}}=\boldsymbol{0}$ se denomina sumidero nodal.
Cuando $a= - 1$, tenemos $y(t)/x(t)=y_0/x_0$ para todo $t$, y por tanto todas las trayectorias son rectas que pasan por el origen. Este es un caso muy especial, ya que las velocidades de desintegración en las dos direcciones son exactamente iguales.
Cuando $a\in\, ]-1,0\, [$, también obtenemos un sumidero nodal pero ahora las soluciones se aproximan al origen a lo largo de la dirección $x$, que es la dirección que decae más lentamente en este caso.
Cuando $a=0$, el sistema es bastante degenerado: $x(t)=x_0$ para todo $t$, por lo que existe toda una línea de puntos fijos, a saber, todo el eje $x$.
Finalmente cuando $a>0$, $\bar{\boldsymbol{x}}$ se vuelve inestable, debido al crecimiento exponencial en la dirección $x$. Vemos que todas las soluciones se desvían del origen y se dirigen al infinito, excepto las que parten del eje $y$ y convergen a él. Aquí $\bar{\boldsymbol{x}}=\boldsymbol{0}$ se llama una silla. El eje $y$ se denomina colector estable del punto de silla $\bar{\boldsymbol{x}}$, definido como el conjunto de condiciones iniciales $\boldsymbol{x}_0$ tales que $\boldsymbol{x}(t)=\bar{\boldsymbol{x}}$ a medida que $t\to+\infty$. Del mismo modo, el colector inestable de $\bar{\boldsymbol{x}}$ es el conjunto de condiciones iniciales tales que $\boldsymbol{x}(t)=\bar{\boldsymbol{x}}$ como $t\to-\infty$. Aquí es el eje $x$.
We can also observe what happens when we reverse time: attractiveness is changed into repulsiveness, and for the saddle point the stable manifold becomes unstable whereas the unstable one becomes stable.
Clasificación de los posibles retratos de fase
Valores propios, vectores propios y soluciones propias.
El ejemplo anterior tiene la particularidad de que dos de las entradas de la matriz $A$ son cero, lo que hace que el sistema esté desacoplado. Por supuesto, queremos estudiar el caso general y obtener una clasificación de todos los posibles retratos de fase. Inspirándonos en ese ejemplo, podemos averiguar cómo proceder. En efecto, los ejes $x$ e $y$ desempeñan un papel geométrico crucial: determinan la dirección de las trayectorias como $t\to \pm \infty$. También contienen trayectorias rectilíneas especiales: una solución que comienza en uno de los ejes de coordenadas permanece en ese eje para siempre, y muestra un crecimiento o decaimiento exponencial simple a lo largo del mismo. ¿Cuál es la analogía en el caso general? Pues bien, nos gustaría encontrar el análogo de las trayectorias rectilíneas, es decir, buscamos soluciones de la forma
$$ \boldsymbol{x}(t)=e^{\lambda t}\boldsymbol{v} $$
where $\boldsymbol{v}\neq \boldsymbol{0}$ is some fixed vector to be determined, and $\lambda$ is a growth rate, also to be determined. If such solutions exist, they correspond to solutions moving exponentially fast along the line spanned by the vector $\boldsymbol{v}$.
Let us find the conditions on $\boldsymbol{v}$ and $\lambda$: we subtitute $\boldsymbol{x}(t)=e^{\lambda t}\boldsymbol{v}$ into $\dot{\boldsymbol{x}}=A\boldsymbol{x}$, and get, after cancelling the nonzero scalar factor $e^{\lambda t}$:
$$ A\boldsymbol{v}=\lambda \boldsymbol{v}. $$
This equation says that the wanted straight line solutions exist if $\boldsymbol{v}$ is an eigenvector of $A$ with corresponding eigenvalue $\lambda$. A solution of the form $\boldsymbol{x}(t)=e^{\lambda t}\boldsymbol{v}$ is called an eigensolution.If you know basic linear algebra, you should not be surprised by the following considerations. In general, the eigenvalues of a matrix $A$ are given by the so-called charateristic function $\text{det}(A-\lambda\mathbb{1})=0$, where $\mathbb{1}$ is the identity matrix ($1$’s on the diagonal entries and $0$’s elsewhere). For $2\times 2$ matrix, this equation is simply
$$ \text{det} \begin{pmatrix} a-\lambda & b\\ c & d-\lambda \end{pmatrix}=0, $$
that is,$$ \lambda^2 -\text{tr}(A)\thinspace\lambda+\text{det}(A)=0 $$
where$$ \text{tr}(A)=a+d,\thinspace \text{det}(A)=ad-bc. $$
The solutions of the characteristic equation are$$ \lambda_1=\frac{\text{tr}(A)+\sqrt{\Delta}}{2},\thinspace\thinspace \lambda_2=\frac{\text{tr}(A)-\sqrt{\Delta}}{2} $$
where$$ \Delta=\text{tr}(A)^2-4\text{det}(A) $$
is the discriminant of the above quadratic equation.We also observe that, by definition of $\lambda_1$ and $\lambda_2$, we have
$$ (\lambda-\lambda_1)(\lambda-\lambda_2)=\lambda^2 -\text{tr}(A)\thinspace\lambda+\text{det}(A)=0 $$
giving by identification$$ \text{det}(A)=\lambda_1\lambda_2, \thinspace\thinspace\text{tr}(A)=\lambda_1+\lambda_2. $$
The typical situation is for the eigenvalues to be distinct: $\lambda_1\neq \lambda_2$. It follows from a general theorem of linear algebra that the corresponding eigenvectors $\boldsymbol{v}_1$ and $\boldsymbol{v}_2$ are linearly independent, and hence span the entire plane.
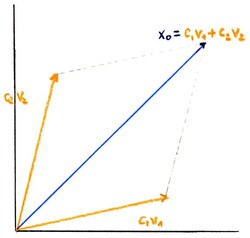
En particular, una condición inicial $\boldsymbol{x}_0$ puede escribirse como una combinación lineal de vectores propios, digamos $\boldsymbol{x}_0=c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2$. Por lo tanto, podemos escribir la solución general para $\boldsymbol{x}(t)$: es
$$ \boldsymbol{x}(t)=c_1\ e^{\lambda_1 t}\boldsymbol{v}_1 + c_2\ e^{\lambda_2 t}\boldsymbol{v}_2. $$
En primer lugar, es una combinación lineal de soluciones de $\dot{\boldsymbol{x}}=A\boldsymbol{x}$, y por lo tanto es en sí misma una solución. En segundo lugar, satisface la condición inicial $\boldsymbol{x}(0)=\boldsymbol{x}_0$, por lo que por el teorema de existencia y unicidad enunciado en la sección anterior, es la única solución.
Vista resumida de todos los retratos de fase.
El siguiente paso es clasificar todos los posibles retratos de fase a medida que varían las entradas de $A$. En el siguiente experimento digital interactivo, mostramos tres vistas que interactúan entre sí: el plano de fase, los valores propios en el plano complejo y el plano $(\text{tr}(A),\text{det}(A))$. Usted puede sintonizar las entradas de $ A $ y ver el retrato de fase resultante, junto con los valores propios correspondientes y el valor correspondiente para $(\text{tr}(A),\text{det}(A))$. Pero también puede mover los valores propios y ver el efecto resultante, o actuar en el plano $(\text{tr}(A),\text{det}(A))$ para ver lo que sucede con el retrato de fase y los valores propios.
La siguiente imagen es un resumen visual de todos los posibles retratos de fase, junto con los nombres dados al punto fijo $\bar{\boldsymbol{x}}=\boldsymbol{0}$ en los diferentes casos que se dan.
Volvamos a los ejemplos presentados anteriormente a la luz de lo que hemos hecho.
Vemos que el origen es un centro para el oscilador armónico. En este caso, $\text{det}(A)=\omega^2$ y $\text{tr}(A)=0$.
Para el circuito RLC tenemos
$$ \text{det}(A)=\frac{1}{L C}>0,\thinspace\thinspace\text{tr}(A)=-\frac{R}{L}\leq 0,\thinspace\thinspace\text{and}\thinspace\thinspace \Delta=\frac{R^2 C-4L}{L^2C}. $$
Así, en el plano $(\text{tr}(A),\text{det}(A))$, estamos en el cuadrante ${\text{tr}(A)\leq 0,\text{det}(A)>0\\}$ (el segundo cuadrante). Si $R=0$ el origen es un centro. Si $R>0$ entonces el origen es un sumidero nodal si $R^2 C-4L>0$, o es un sumidero espiral si $R^2 C-4L<0$. Cuando $R^2 C-4L=0$ tenemos un sumidero nodal degenerado.
Para el tercer ejemplo tenemos
$$ \text{det}(A)=-a, \thinspace\thinspace\text{tr}(A)=a-1. $$
Cuando $a>0$, el origen es una silla de montar. Cuando $a<0$, es un sumidero nodal.
Más información sobre la clasificación.
El experimento digital interactivo anterior y la imagen asociada reúnen de forma compacta toda la información sobre el comportamiento de las soluciones y la geometría de las trayectorias correspondientes de ecuaciones diferenciales lineales bidimensionales. En particular, podemos ver cómo las soluciones son atraídas o repelidas por el origen. Aquí analizamos lo que hay detrás de estas imágenes desde un punto de vista matemático. El lector impaciente puede saltarse esta sección y volver más adelante.
Toda la información que necesitamos está contenida en las siguientes fórmulas que hemos obtenido anteriormente:
$$ \lambda_{1,2}=\frac{\text{tr}(A)\pm\sqrt{\text{tr}(A)^2-4\text{det}(A)}}{2} \thinspace,\thinspace\thinspace \text{det}(A)=\lambda_1\lambda_2, \thinspace\thinspace \text{tr}(A)=\lambda_1+\lambda_2. $$
- Si $\text{det}(A)<0$, significa que los valores propios son distintos, reales y de signos opuestos. La eigensolución correspondiente al valor propio negativo decrece exponencialmente. La eigensolución correspondiente al valor propio positivo crece exponencialmente. Esto significa que el origen es una silla.
- Si $\text{det}(A)>0$, los valores propios son reales con el mismo signo (sumideros/fuentes nodales), o complejos conjugados (sumideros/fuentes espirales y centros). Los sumideros/fuentes nodales satisfacen $\text{tr}(A)^2-4\text{det}(A)>0$ y los sumideros/fuentes espirales satisfacen $\text{tr}(A)^2-4\text{det}(A)<0$. La diferencia entre sumideros y fuentes viene dada por el signo de $\text{tr}(A)$: cuando $\text{tr}(A)<0$, ambos valores propios tienen partes reales negativas y tenemos un sumidero, y, cuando $\text{tr}(A)>0$, ambos valores propios tienen partes reales positivas y tenemos una fuente. Los centros viven en la frontera $\text{tr}(A)=0$, donde los valores propios son puramente imaginarios. Otra frontera viene dada por la parábola $\text{tr}(A)^2-4\text{det}(A)=0$ donde viven sumideros/fuentes nodales degenerados, y sumideros/fuentes nodales especiales para los que los dos valores propios son iguales.
- Si $\text{det}(A)=0$, al menos uno de los valores propios es cero. Entonces el origen no es un punto fijo aislado. Hay una línea entera de puntos fijos, o un plano de puntos fijos si $A=0$.
Está claro que las sillas de montar, los sumideros/fuentes nodales y los sumideros/fuentes en espiral son los casos genéricos porque se dan en grandes regiones abiertas del plano $(\text{tr}(A),\text{det}(A))$. Los demás casos, como los centros o los sumideros/fuentes nodales degenerados, son casos límite y no son `robustos’: si, por ejemplo, estamos en la parábola $\text{tr}(A)^2-4\text{det}(A)=0$, la abandonamos en cuanto modificamos muy ligeramente las entradas de $A$. De los casos límite, los centros siguen siendo importantes en el contexto de los sistemas mecánicos sin fricción en los que se conserva la energía (por ejemplo, el oscilador armónico).
Clasificación dinámica: sillas de montar, sumideros y fuentes.
Si sólo nos interesa el comportamiento a largo plazo de las soluciones, la clasificación anterior resulta demasiado sofisticada. En efecto, un sumidero nodal no es muy diferente de un sumidero en espiral: en ambos casos, las soluciones son atraídas hacia él. Teniendo en cuenta este tipo de consideraciones, podemos acabar con tres categorías:
- sillas de montar (un valor propio es positivo y el otro negativo);
- sumideros (ambos valores propios tienen partes reales negativas);
- fuentes (ambos valores propios tienen partes reales positivas).
Obsérvese que en estos tres casos, los valores propios tienen partes reales distintas de cero.

