Nous avons dit précédemment que la plupart des équations différentielles ne peuvent pas être résolues explicitement. Ce n’est pas complètement vrai : les équations différentielles linéaires peuvent être analysées de manière approfondie. La plupart des modèles en physique, biologie, etc, sont des équations différentielles non linéaires, mais celles qui sont linéaires jouent un rôle important dans la classification de leurs points fixes, comme on le verra au chapitre suivant.
Définition
Un système linéaire à deux dimensions est un système de la forme
$$ \begin{cases} \dot{x}= ax+by\\ \dot{y}= cx+dy \end{cases} $$
où $a,b,c,d$ sont des paramètres. En notation vectorielle, ceci s’écrit de manière plus compacte sous forme de matrice comme suit$$ \dot{\boldsymbol{x}}=A\boldsymbol{x} $$
où$$ A= \begin{pmatrix} a & b\\ c & d \end{pmatrix} \hspace{0.5cm}\text{and}\hspace{0.5cm} \boldsymbol{x}= \begin{pmatrix} x\\ y \end{pmatrix}\, . $$
De tels systèmes sont la version bidimensionnelle naturelle de l’équation scalaire $\dot{x}=ax$ qui est la première que nous avons vue dans cet ebook. Nous disons qu’elle est linéaire car si $\boldsymbol{x}_1$ et $\boldsymbol{x}_2$ sont des solutions, alors toute combinaison linéaire $c_1 \boldsymbol{x}_1+ c_2 \boldsymbol{x}_2$, où $c_1, c_2$ sont des nombres réels, l’est aussi. Remarquez que $\dot{\boldsymbol{x}}=\boldsymbol{0}$ lorsque $\boldsymbol{x}=\boldsymbol{0}$, donc $\bar{\boldsymbol{x}}=\boldsymbol{0}$ est toujours un point fixe pour tout choix de $A$.Exemples
Retour à l’oscillateur harmonique.
Nous avons déjà rencontré un exemple d’équation différentielle linéaire à deux dimensions, à savoir l’oscillateur harmonique. Rappelons qu’il s’agit d’une particule de masse $m$ se déplaçant sur l’axe $x$ soumise à la force $f(x)=-kx$. Comme nous l’avons vu, l’équation de mouvement $\ddot x=-kx$ peut être représentée comme un système linéaire bi-dimensionnel $\dot{\boldsymbol{x}}=A\boldsymbol{x}$ avec
$$ A= \begin{pmatrix} 0 & 1\\ -\omega^2 & 0 \end{pmatrix} $$
où $\omega^2=\frac{k}{m}$. Nous pouvons ajouter une force de friction de la forme $-\epsilon \dot{x}$, où $\epsilon>0$, ce qui donne un système linéaire à deux dimensions avec$$ A= \begin{pmatrix} 0 & 1\\ -\omega^2 & -\epsilon \end{pmatrix}. $$
On voit que, lorsque $\epsilon=0$, toutes les trajectoires sont fermées et encerclent l’origine (l’unique point fixe) qui est appelée un centre. Lorsque $\epsilon>0$, les trajectoires ne sont plus fermées : les solutions spiralent vers l’origine.
Circuits électriques.
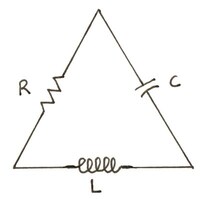
Considérons maintenant un circuit RLC en série, où $R$ représente la résistance, $L$ l’inductance et $C$ le condensateur. Dans ce modèle, la résistance est seule responsable de la dissipation d’énergie, tandis que l’inducteur et le condensateur sont idéalisés comme étant capables de stocker de l’énergie sans dissipation.
En supposant que le circuit possède une source d’énergie affichant une tension constante dans le temps, nous pouvons appliquer la loi du courant de Kirchhoff, la loi de Faraday et la loi d’Ohm pour obtenir l’équation différentielle du second ordre
$$ L \ddot{I}+R\dot{I}+\frac{I}{C}=0 $$
où $I(t)$ est le courant dans le circuit et $L,C>0$ et $R\geq 0$ sont des paramètres. La loi d’Ohm dit que la tension aux bornes de la résistance est proportionnelle au courant, la constante de proportionnalité étant $R$. Cette relation rend le système linéaire. De nombreuses résistances obéissent à la loi d’Ohm. (Observez que lorsque $R=0$, nous obtenons une équation qui est formellement la même que celle de l’oscillateur harmonique). Nous pouvons réécrire l’équation sous la forme d’une équation différentielle linéaire à deux dimensions en fixant $x=I$ et $y=\dot{x}$. Cela donne$$ \begin{cases} \dot{x}= y\\ \dot{y}= - \frac{1}{L C}\thinspace x-\frac{R}{L} y \end{cases} $$
donc$$ A= \begin{pmatrix} 0 & 1\\ - \frac{1}{L C} & -\frac{R}{L} \end{pmatrix}. $$
Au passage, on observe que le système obtenu pour le circuit RLC a exactement la même forme que celui décrivant un oscillateur harmonique amorti si on identifie $\frac{1}{L C}$ à $\omega^2$ et $\frac{R}{L}$ à $\epsilon$. En effet, $R=0$ correspond à un circuit idéal dans lequel il n’y aurait pas de dissipation d’énergie par effet Joule.
Un exemple abstrait.
Nous considérons maintenant le système linéaire
$$ \begin{cases} \dot{x}= a x\\ \dot{y}= -y \end{cases} $$
où $a\in\mathbb{R}$ est un paramètre. En notation vectorielle, cela signifie que $\dot{\boldsymbol{x}}=A\boldsymbol{x}$ avec$$ A= \begin{pmatrix} a & 0\\ 0 & -1 \end{pmatrix}. $$
Les deux équations sont découplées dans le sens où il n’y a pas de $x$ dans l’équation $y$ et vice versa. Cela implique que chaque équation peut être résolue séparément. Nous obtenons facilement$$ x(t)=x_0 e^{at},\thinspace y(t)=y_0 e^{-t}. $$
La géométrie des trajectoires au voisinage de l’origine, qui est un point fixe pour toute valeur de $a$, peut être explorée avec l’expérience numérique interactive suivante.
Commentons ce que nous observons.
La composante $y(t)$ décroît exponentiellement avec $t$ quelle que soit la valeur de $a$. Lorsque $a<0$, $x(t)$ décroît aussi exponentiellement et donc toutes les trajectoires s’approchent de l’origine quand $t\to+\infty$. Cependant, la direction de l’approche dépend de la taille de $a$ par rapport à $-1$.
Lorsque $a<-1$, $x(t)$ décroît plus rapidement que $y(t)$. Les solutions s’approchent de l’origine tangente à la direction la plus lente, c’est-à-dire la direction $y$. Le point fixe $\bar{\boldsymbol{x}}=\boldsymbol{0}$ est appelé un puits nodal.
Lorsque $a= - 1$, on a $y(t)/x(t)=y_0/x_0$ pour tout $t$, et donc toutes les trajectoires sont des droites passant par l’origine. Il s’agit d’un cas très particulier puisque les taux de décroissance dans les deux directions sont exactement égaux.
Lorsque $a\in\, ]-1,0\, [$, nous obtenons également un puits nodal mais les solutions s’approchent maintenant de l’origine le long de la direction $x$, qui est la direction de décroissance la plus lente dans ce cas.
Lorsque $a=0$, le système est tout à fait dégénéré : $x(t)=x_0$ pour tout $t$, il existe donc une ligne entière de points fixes, à savoir l’axe $x$ entier.
Enfin lorsque $a>0$, $\bar{\boldsymbol{x}}$ devient instable, à cause de la croissance exponentielle dans la direction $x$. Nous constatons que toutes les solutions s’écartent de l’origine et se dirigent vers l’infini, sauf celles qui partent de l’axe $y$ et qui y convergent. On appelle ici $\bar{\boldsymbol{x}}=\boldsymbol{0}$ un point-selle. L’axe $y$ est appelé variété stable du point-selle $\bar{\boldsymbol{x}}$, défini comme l’ensemble des conditions initiales $\boldsymbol{x}_0$ telles que $\boldsymbol{x}(t)=\bar{\boldsymbol{x}}$ quand $\to+\infty$. De même, la variété instable de $\bar{\boldsymbol{x}}$ est l’ensemble des conditions initiales telles que $\boldsymbol{x}(t)=\bar{\boldsymbol{x}}$ quand $t\to-\infty$. Il s’agit ici de l’axe $x$.
On peut aussi observer ce qui se passe lorsqu’on « inverse le temps » (on change $t$ en $-t$) : l’attraction se transforme en répulsion, et pour le point-selle, la variété stable devient instable alors que celui qui est instable devient stable.
Classification des portraits de phase possibles
Valeurs propres, vecteurs propres et solutions propres.
L’exemple précédent présente la particularité que deux des coefficients de la matrice $A$ sont nuls, ce qui rend le système découplé. Bien sûr, nous voulons étudier le cas général et obtenir une classification de tous les portraits de phase possibles. En nous inspirant de cet exemple, nous pouvons déterminer comment procéder. En effet, les axes $x$ et $y$ jouent un rôle géométrique crucial : ils déterminent la direction des trajectoires quand $t\to \pm \infty$. Ils contiennent également des trajectoires spéciales qui sont des droites : une solution commençant sur l’un des axes de coordonnées reste sur cet axe pour toujours, et présente une simple croissance ou décroissance exponentielle le long de celui-ci. Quel est l’analogue dans le cas général ? Eh bien, nous voudrions trouver l’analogue des trajectoires qui sont des droites, c’est-à-dire que nous cherchons des solutions de la forme
$$ \boldsymbol{x}(t)=e^{\lambda t}\boldsymbol{v} $$
où $\boldsymbol{v}\neq \boldsymbol{0}$ est un vecteur à déterminer et $\lambda$ est un taux de croissance, également à déterminer. Si de telles solutions existent, elles correspondent à des solutions se déplaçant exponentiellement vite le long de la droite définie par le vecteur $\boldsymbol{v}$.Trouvons les conditions sur $\boldsymbol{v}$ et $\lambda$ : on substitue $\boldsymbol{x}(t)=e^{\lambda t}\boldsymbol{v}$ dans $\dot{\boldsymbol{x}}=A\boldsymbol{x}$, et on obtient, après simplification par le facteur scalaire non nul $e^{\lambda t}$ :
$$ A\boldsymbol{v}=\lambda \boldsymbol{v}. $$
Cette équation dit que les solutions rectilignes recherchées existent si $\boldsymbol{v}$ est un vecteur propre de $A$ avec la valeur propre correspondante $\lambda$ correspondante. Une solution de la forme $\boldsymbol{x}(t)=e^{\lambda t}\boldsymbol{v}$ est appelée une solution propre.Si vous connaissez les bases de l’algèbre linéaire, vous ne devriez pas être surpris par les considérations suivantes. En général, les valeurs propres d’une matrice $A$ sont données par ce que l’on appelle l’équation caractéristique $\text{det}(A-\lambda\mathbb{1})=0$, où $\mathbb{1}$ est la matrice identité (des $1$ sur les coefficients diagonaux et des $0$ ailleurs). Pour une matrice $2\times 2$, cette équation est simplement
$$ \text{det} \begin{pmatrix} a-\lambda & b\\ c & d-\lambda \end{pmatrix}=0, $$
c’est-à-dire
$$ \lambda^2 -\text{tr}(A)\thinspace\lambda+\text{det}(A)=0 $$
où$$ \text{tr}(A)=a+d, \thinspace \text{det}(A)=ad-bc. $$
Les solutions de l’équation caractéristique sont$$ \lambda_1=\frac{\text{tr}(A)+\sqrt{\Delta}}{2},\thinspace\thinspace \lambda_2=\frac{\text{tr}(A)-\sqrt{\Delta}}{2} $$
où$$ \Delta=\text{tr}(A)^2-4\text{det}(A) $$
est le discriminant de l’équation quadratique ci-dessus.On observe également que, par définition de $\lambda_1$ et $\lambda_2$, on a
$$ (\lambda-\lambda_1)(\lambda-\lambda_2)=\lambda^2 -\text{tr}(A)\thinspace\lambda+\text{det}(A)=0 $$
donnant par identification$$ \text{det}(A)=\lambda_1\lambda_2, \thinspace\thinspace\text{tr}(A)=\lambda_1+\lambda_2. $$
La situation typique est celle où les valeurs propres sont distinctes : $\lambda_1\neq \lambda_2$. Il résulte d’un théorème général d’algèbre linéaire que les vecteurs propres correspondants $\boldsymbol{v}_1$ et $\boldsymbol{v}_2$ sont linéairement indépendants, et donc engendrent le plan.
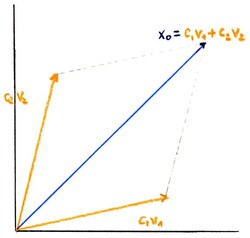
En particulier, une condition initiale $\boldsymbol{x}_0$ peut être écrite comme une combinaison linéaire de vecteurs propres, disons $\boldsymbol{x}_0=c_1\boldsymbol{v}_1+c_2\boldsymbol{v}_2$. Par conséquent, nous pouvons écrire la solution générale de $\boldsymbol{x}(t)$ : c’est
$$ \boldsymbol{x}(t)=c_1\ e^{\lambda_1 t}\boldsymbol{v}_1 + c_2\ e^{\lambda_2 t}\boldsymbol{v}_2. $$
Premièrement, il s’agit d’une combinaison linéaire de solutions de $\dot{\boldsymbol{x}}=A\boldsymbol{x}$, et donc d’une solution en soi. Deuxièmement, elle satisfait la condition initiale $\boldsymbol{x}(0)=\boldsymbol{x}_0$, et donc par le théorème d’existence et d’unicité énoncé dans la section précédente, c’est la seule solution.Vue synthétique de tous les portraits de phase.
L’étape suivante consiste à classer tous les portraits de phase possibles lorsque les coefficients de $A$ varient. Dans l’expérience numérique interactive suivante, nous affichons trois vues qui interagissent entre elles : le plan de phase, les valeurs propres dans le plan complexe et le plan $(\text{tr}(A),\text{det}(A))$. Vous pouvez soit changer les entrées de $A$ et voir le portrait de phase résultant, ainsi que les valeurs propres correspondantes et la valeur correspondante pour $(\text{tr}(A),\text{det}(A))$. Mais vous pouvez aussi déplacer les valeurs propres et voir l’effet résultant, ou agir dans le plan $(\text{tr}(A),\text{det}(A))$ pour voir ce qui arrive au portrait de phase et aux valeurs propres.
Le schéma suivant est un résumé visuel de tous les portraits de phase possibles, ainsi que les noms donnés au point fixe $\bar{\boldsymbol{x}}=\boldsymbol{0}$ dans les différents cas qui se présentent.
Reprenons les exemples présentés ci-dessus à la lumière de ce que nous venons de faire.
Nous voyons que l’origine est un centre pour l’oscillateur harmonique. Dans ce cas, $\text{det}(A)=\omega^2$ et $\text{tr}(A)=0$.
Pour le circuit RLC, nous avons
$$ \text{det}(A)=\frac{1}{L C}>0,\thinspace\thinspace\text{tr}(A)=-\frac{R}{L}\leq 0,\thinspace\thinspace\text{et}\thinspace \Delta=\frac{R^2 C-4L}{L^2C}. $$
Ainsi, dans le plan $(\text{tr}(A),\text{det}(A))$, on se trouve dans le quadrant $\{\text{tr}(A)\leq 0,\text{det}(A)>0\}$ (le deuxième quadrant). Si $R=0$ l’origine est un centre. Si $R>0$ alors l’origine est soit un puits nodal si $R^2 C-4L>0$, soit un puits spiralé si $R^2 C-4L<0$. Lorsque $R^2 C-4L=0$, nous avons un puits nodal dégénéré.Pour le troisième exemple, nous avons
$$ \text{det}(A)=-a, \thinspace\thinspace\text{tr}(A)=a-1. $$
Lorsque $a>0$, l’origine est un point-selle. Lorsque $a<0$, elle est un puits nodal.En savoir plus sur la classification.
L’expérience numérique interactive précédente et le schéma rassemblent de manière compacte toutes les informations sur le comportement des solutions et la géométrie des trajectoires correspondantes des équations différentielles linéaires bi-dimensionnelles. En particulier, nous pouvons voir comment les solutions sont attirées ou repoussées par l’origine. Nous analysons ici ce qui se cache derrière ces images d’un point de vue mathématique. Le lecteur impatient peut sauter cette section et y revenir plus tard.
Toutes les informations dont nous avons besoin sont contenues dans les formules suivantes que nous avons obtenues ci-dessus :
$$ \lambda_{1,2}=\frac{\text{tr}(A)\pm\sqrt{\text{tr}(A)^2-4\text{det}(A)}}{2} \thinspace,\thinspace\thinspace \text{det}(A)=\lambda_1\lambda_2, \thinspace\thinspace \text{tr}(A)=\lambda_1+\lambda_2. $$
- Si $\text{det}(A)<0$, cela signifie que les valeurs propres sont distinctes, réelles et de signes opposés. La solution propre correspondant à la valeur propre négative décroît exponentiellement. La solution propre correspondant à la valeur propre positive croît exponentiellement. Cela signifie que l’origine est un point-selle (ou col).
- Si $\text{det}(A)>0$, les valeurs propres sont soit réelles avec le même signe (puits/sources nodaux), soit complexes conjuguées (puits/sources spirales et centres). Les puits/sources nodaux satisfont à $\text{tr}(A)^2-4\text{det}(A)>0$ et les puits/sources spirales satisfont à $\text{tr}(A)^2-4\text{det}(A)<0$. La différence entre les puits et les sources est donnée par le signe de $\text{tr}(A)$ : lorsque $\text{tr}(A)<0$, les deux valeurs propres ont une partie réelle négative et nous avons un puits, et, lorsque $\text{tr}(A)>0$, les deux valeurs propres ont une partie réelle positive et nous avons une source. Les centres se situent à la « frontière » $\text{tr}(A)=0$, où les valeurs propres sont purement imaginaires. Une autre frontière est donnée par la parabole $\text{tr}(A)^2-4\text{det}(A)=0$ qui correspondent aux puits/sources nodaux dégénérés, et des puits/sources nodaux spéciaux pour lesquels les deux valeurs propres sont égales.
- Si $\text{det}(A)=0$, au moins une des valeurs propres est nulle. Alors l’origine n’est pas un point fixe isolé. Il existe soit une ligne entière de points fixes, soit un plan de points fixes si $A=0$.
Il est clair que les points-selles, les puits/sources nodaux et les puits/sources spirales sont les cas génériques car ils se produisent dans de grandes régions ouvertes du plan $(\text{tr}(A),\text{det}(A))$. Les autres cas, comme les centres ou les puits/sources nodaux dégénérés, sont des cas limites et ne sont pas `robustes’ : si, par exemple, nous sommes sur la parabole $\text{tr}(A)^2-4\text{det}(A)=0$, alors nous la quittons dès que nous modifions très légèrement les coefficients de $A$. Parmi les cas limites, les centres sont tout de même importants dans le contexte des systèmes mécaniques sans frottement où l’énergie est conservée (par exemple, l’oscillateur harmonique).
Classification dynamique : selles, puits et sources.
Si l’on s’intéresse uniquement au comportement à long terme des solutions, la classification précédente est un peu trop précise. En effet, un puits nodal n’est pas très différent d’un puits spirale : dans les deux cas, les solutions sont attirées vers lui. Avec ce genre de considération en tête, on peut aboutir à trois grandes catégories :
- les points-selles (une valeur propre est positive et l’autre est négative) ;
- les puits (les deux valeurs propres ont des parties réelles négatives) ;
- les sources (les deux valeurs propres ont des parties réelles positives).
Observez que dans ces trois cas, les valeurs propres ont des parties réelles non nulles.

