Nous présentons divers exemples où des cycles limites attractifs apparaissent.
Nous avons jusqu’à présent étudié la chose la plus simple que peut faire une solution d’une équation différentielle : être attirée ou repoussée par un point fixe. La prochaine chose la plus simple qu’elle puisse faire est de se comporter périodiquement dans le temps, c’est-à-dire de tracer une courbe fermée, appelée cycle. Nous avons déjà rencontré des exemples de solutions périodiques dans la première partie de cet ebook. En particulier, nous avons vu un exemple de cycle limite stable ou attractif. Il correspond à des oscillations auto-entretenues qui sont robustes sous de légères perturbations. De tels cycles limites apparaissent dans des systèmes physiques, biologiques et chimiques. Nous verrons que ces objets n’apparaissent que dans les systèmes non linéaires.
Solutions et cycles périodiques
Considérons un système bi-dimensionnel
$$ \begin{cases} \dot{x}=f(x,y)\\ \dot{y}=g(x,y) \end{cases} $$
où $(x,y)\in\mathbb{R}^2$ et $f,g :\mathbb{R}^2\to\mathbb{R}$ sont des fonctions continûment différentiables. Nous disons qu’une solution $(x(t),y(t))$ est périodique s’il existe un certain nombre $T>0$ tel que $x(t)=x(t+T)$ et $y(t)=y(t+T)$ pour tout nouvel espace $t$.La période de cette solution est définie comme le plus petit $T$ ayant cette propriété. La trajectoire d’une solution périodique est une courbe fermée dans le plan $xy$ (« cycle »). Remarquez qu’une solution constante (c’est-à-dire un point fixe) n’est pas considérée comme une solution périodique.
Remarque.
Pour définir les solutions périodiques, il suffit d’exiger qu’il existe un temps $T>0$ tel que $x(0)=x(T)$ et $y(0)=y(T)$. Alors, par l’énoncé sur l’unicité des solutions des équations différentielles, nous devons avoir $x(t)=x(t+T)$ et $y(t)=y(t+T)$ pour tout $t$.
Les cycles ne peuvent pas être isolés pour les systèmes linéaires.
L’exemple le plus simple que nous ayons rencontré est l’oscillateur harmonique décrit par le système linéaire
$$ \begin{cases} \dot{x}= y \\ \dot{y}=-x. \end{cases} $$
Nous constatons qu’aucun des cycles n’est isolé. Il s’agit en fait d’une caractéristique générale des systèmes linéaires. En effet, supposons que l’on nous donne un système linéaire $\dot{\boldsymbol{x}}=A\boldsymbol{x}$ tel qu’il existe une solution périodique $\boldsymbol{x}(t)$. Alors il en est de même pour $c\thinspace\boldsymbol{x}(t)$ pour toute constante $c\neq 0$, par linéarité. Par conséquent, le cycle associé à $\boldsymbol{x}(t)$ est entouré d’une famille de cycles à un paramètre. En particulier, l’amplitude d’une oscillation périodique est entièrement fixée par sa condition initiale $\boldsymbol{x}_0$. Et toute petite perturbation de l’amplitude persistera éternellement. En revanche, nous allons voir que, dans les systèmes non linéaires, il est possible d’avoir des cycles isolés qui contrôlent le comportement des trajectoires proches.
Cycles limites
Supposons que nous ayons un système non linéaire $\dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x})$ avec un cycle isolé $C$. Par "isolé", nous voulons dire qu’il n’existe pas d’autre cycle, du moins dans un voisinage annulaire suffisamment petit de $C$. Nous nous attendons à ce que les trajectoires suffisamment proches ressentent sa présence. Que peut-il se passer ? Eh bien, elles peuvent soit s’approcher de $C$, soit s’en éloigner. Alors $C$ est appelé un cycle limite.
Il est naturel de dire que $C$ est stable ou attractif si les trajectoires proches spiralent vers $C$ des deux côtés. Lorsqu’elles s’éloignent de $C$ des deux côtés, on dit que $C$ est instable ou répulsif. Dans le cas mixte, nous disons que $C$ est semi-stable. Ce troisième cas n’est pas générique.
Construire un cycle limite de toutes pièces. Nous voulons créer un exemple simple de cycle limite, une sorte de modèle jouet. Cherchons un système dont le cercle de rayon un centré sur $(0,0)$ est un cycle limite attracteur. L’astuce consiste à penser en termes de coordonnées polaires $(r,\theta)$. La situation la plus simple serait d’avoir des équations non couplées pour les mouvements radiaux et angulaires :
$$ \begin{cases} \dot{r}=f(r)\\ \dot{\theta}=g(\theta). \end{cases} $$
Dans la direction $r$, nous voulons que $f(1)=0$, c’est-à-dire que $r=1$ soit un point fixe. Nous voulons également que $r(t)$ diminue jusqu’à $1$ si $r(0)>1$, et augmente jusqu’à $1$ si $r(0)<1$. Prenons l’équation logistique, c’est-à-dire$$ \dot{r}=r(1-r). $$
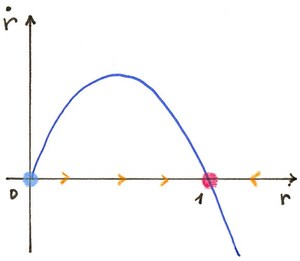
Dans la direction $\theta$, nous pouvons simplement prendre une rotation à vitesse angulaire constante, par exemple $\dot{\theta}=-1$ pour une rotation dans le sens horaire. En combinant les mouvements radiaux et angulaires, on obtient des trajectoires en spirale vers le cercle, des deux côtés.
En revenant aux coordonnées cartésiennes, cela donne des équations beaucoup plus compliquées qui sont couplées :
$$ \begin{cases} \dot{x}= y +x\big(1-\sqrt{x^2+y^2}\big) \dot{y}=-x+ y\big(1-\sqrt{x^2+y^2}\big). \end{cases} $$
Avec la recette précédente, nous pouvons préparer des exemples avec, disons, trois cycles limites :
$$ \begin{cases} \dot{r}= r(1-r)(2-r)(3-r)\\ \dot{\theta}=-1. \end{cases} $$
Les cercles de rayon $1$ et $3$ sont des cycles limites stables, alors que le cercle de rayon $2$ est un cycle instable.
Nous avons donc facilement réalisé des exemples de cycles limites à partir de rien. Mais, en pratique, nous sommes confrontés au problème inverse : étant donné un champ de vecteurs $\boldsymbol{f}$, comment savons-nous qu’il engendre un cycle limite ? Pouvons-nous prédire le nombre de cycles limites qu’il aura ? Bien sûr, nous pouvons utiliser des expériences numériques. Mathématiquement parlant, prouver l’existence d’un cycle limite peut être difficile. Prédire combien de cycles limites il peut y avoir s’avère être un problème ouvert, même pour les champs de vecteurs polynomiaux !
Prévenir la présence d’un cycle limite.
Bien que les cycles limites apparaissent assez naturellement dans les modèles physiques, biologiques ou chimiques, il n’est pas facile de mathématiquement prouver l’existence d’un cycle limite. L’outil principal pour le faire est la théorie dite de Poincaré-Bendixson. Nous énonçons délibérément le théorème suivant de manière informelle, et non dans sa forme la plus générale.
Théorème de Poincaré-Bendixson.Considérons un système$$ \begin{cases} \dot{x}=f(x,y)\\ \dot{y}=g(x,y) \end{cases} $$
où $f$ et $g$ ont des dérivées partielles continues, et telles que des solutions existent pour tout $t$. Soit $R$ une région fermée et bornée du plan $xy$ qui ne contient aucun point fixe. Supposons qu’aucune solution ne puisse quitter $R$. Alors le système a une solution périodique dans la région $R$.
Il est courant d’appeler la région $R$ une région de piégeage, puisque, si et quand une solution quelconque entre dans $R$, elle ne peut plus en sortir. Ainsi, pour appliquer le théorème, notre tâche consiste à trouver une région telle que, si nous nous déplaçons le long de ses limites, nous sommes toujours poussés dans la région. Mathématiquement, cela signifie que le champ de vecteurs pointe vers l’intérieur le long de la frontière délimitant $R$. Il est en général difficile de trouver une région de piégeage. Nous verrons des exemples dans la suite.

Une conséquence du théorème de Poincaré-Bendixson est que s’il existe une trajectoire fermée dans un système à deux dimensions, alors elle doit contenir un point fixe.
D’un point de vue intuitif, le théorème de Poincaré-Bendixson est un résultat plutôt plausible. En effet, toute solution commençant en $R$ y reste pour toujours, et elle ne peut pas s’approcher d’un point fixe. Elle ne peut pas tendre vers l’infini puisque $R$ est borné, par hypothèse. Maintenant, prenons un point $(x_0,y_0)$ à l’intérieur de $R$ et lançons la solution correspondante. Si à un certain moment $t>0$ nous avons $(x(t),y(t))=(x_0,y_0)$, alors cela signifie que nous avons une solution périodique. Si un tel temps n’existe pas, il existe deux scénarios puisqu’une trajectoire ne peut pas s’auto-intersecter. Soit la solution finit par tourner, par exemple dans le sens des aiguilles d’une montre, soit elle doit faire un nombre infini de tours pour changer le sens de sa rotation. Dans le premier cas, elle doit "s’écraser" sur une trajectoire fermée. Dans le second cas, comme la trajectoire ne peut pas s’auto-intersecter, cela implique que les virages deviennent de plus en plus nets ; à long terme, cela contredit la différentiabilité du champ de vecteurs. Cependant, une preuve rigoureuse du théorème de Poincaré-Bendixson est assez longue et nécessite toute la force d’un théorème de topologie d’apparence innocente, à savoir le théorème de Jordan.
Avertissement. Le théorème de Poincaré-Bendixson ne se généralise pas à trois dimensions ou plus. Nous verrons plus loin les conséquences considérables de ce fait.
Exclure la présence d’un cycle limite
Nous présentons maintenant les outils qui peuvent être utilisés pour éliminer la possibilité d’avoir des cycles.
Théorème de Bendixson. Considérons un système$$ \begin{cases} \dot{x}=f(x,y)\\ \dot{y}=g(x,y) \end{cases} $$
où $f$ et $g$ ont des dérivées partielles continues sur un domaine simplement connecté $D$ du plan $xy$. (Par « simplement connexe » nous voulons dire que le domaine n’a pas de « trous » ou de portions disjointes). Alors, si la quantité$$ \frac{\partial f}{\partial x}(x,y)+\frac{\partial g}{\partial y}(x,y) $$
n’est pas identiquement nulle (c’est-à-dire, non nulle pour tout $(x,y)$ dans $D$) et est de signe unique dans $D$, il n’y a pas de cycles à l’intérieur de $D$.
Donnons la preuve de ce théorème qui est par contradiction. Supposons que nous ayons bien une trajectoire fermée $C$, d’intérieur $I$, contenue dans $D$.

On applique le théorème de Green qui dit que
$$ \oint_C (f\boldsymbol{i}+g\boldsymbol{j})\cdot \boldsymbol{n}\, \text{d}s \equiv \oint_C f\text{d}y-g\text{d}x = \iint_I \left( \frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}\right) \, \text{d}x\, \text{d}y $$
où $\boldsymbol{i}$ (resp. $\boldsymbol{j}$) est le vecteur unitaire dans la direction $x$ (resp. dans la direction $y$), et $\boldsymbol{n}$ est la normale sortante à la courbe $C$. Par hypothèse, l’intégrande du côté droit est continue et jamais nulle ; elle est donc soit toujours positive, soit toujours négative, et le côté droit est donc soit positif, soit négatif. D’autre part, le membre de gauche doit être nul. Car puisque $C$ est une trajectoire fermée, $C$ est toujours tangent au champ de vecteurs $f\boldsymbol{i}+g\boldsymbol{j}$. Cela signifie que $\boldsymbol{n}$ est toujours perpendiculaire à $f\boldsymbol{i}+g\boldsymbol{j}$, de sorte que l’intégrande $(f\boldsymbol{i}+g\boldsymbol{j})\cdot \boldsymbol{n}$ est identiquement nulle. On est donc arrivé à une contradiction, on en conclut qu’il ne peut pas exister de trajectoire fermée dans $D$.
Remarque.
La quantité apparaissant dans le théorème de Dulac n’est rien d’autre que la divergence du champ de vecteurs. Rappelez-vous notre interprétation d’une équation différentielle comme décrivant un écoulement de fluide imaginaire : le champ de vecteurs donne la vitesse du fluide en chaque point $(x,y)$. Alors, la divergence du champ de vecteurs décrit dans quelle mesure l’écoulement se comporte comme une source ou un puits en $(x,y)$. Il s’agit d’une mesure locale quantifiant s’il y a plus de « particules » qui sortent d’une région infinitésimale de l’espace que de choses qui y entrent. On peut voir que la divergence du champ de vecteurs en un point $(x,y)$ est la trace de la matrice jacobienne en ce point.
Exemple. Considérons un système linéaire général à deux dimensions
$$ \begin{cases} \dot{x}=ax+by\\ \dot{y}= cx+dy \end{cases} $$
où $a,b,c,d$ sont des paramètres réels. En appliquant le théorème de Bendixson, on trouve que si $a+d\neq 0$ alors il n’y a pas de trajectoire fermée. Si $a+d=0$, ce théorème ne dit rien. Mais nous pouvons facilement conclure en utilisant ce que nous avons appris sur les systèmes linéaires. La fonction caractéristique du système est
$$ \lambda^2 -(a+d)\lambda +(ad-bc)=0. $$
Si $a+d=0$ alors les solutions sont de signe opposé si $ad-bc<0$ et l’origine est un point-selle. Si $ad-bc>0$ alors les solutions sont purement imaginaires et l’origine est un centre. Dans le cas particulier $a=d=0$, $b=1$, $c=-1$, on obtient l’oscillateur harmonique $\dot{x}=y$, $\dot{y}=-x$ pour lequel on sait maintenant qu’il existe un continuum de trajectoires fermées. En conclusion, le système linéaire ci-dessus possède des cycles si, et seulement si, $a+d=0$, $ad-bc>0$.
Malheureusement, le théorème de Bendixson peut s’avérer inapplicable même pour des systèmes simples. Mais Dulac a judicieusement généralisé ce théorème en faisant l’observation simple mais profonde suivante : considérons le système
$$ \begin{cases} \dot{x}= \varphi(x,y)\, f(x,y)\\ \dot{y}= \varphi(x,y)\, g(x,y) \end{cases} $$
où $\varphi$ est une fonction continûment différentiable, à valeurs réelles ; elle partage le même portrait de phase que le système
$$ \begin{cases} \dot{x}= f(x,y)\\ \dot{y}= g(x,y). \end{cases} $$
$$
\frac{\text{d} x}{\text{d}(\varphi(x,y)t)}=f(x,y).
$$
Pensez au cas où $\varphi(x,y)>0$ pour tout $(x,y)$. Prenez alors l’équation ci-dessus pour $\dot{x}$ ; elle peut s’écrire comme suit
Dès lors, si on peut réfuter l’existence d’une trajectoire fermée pour un certain $\varphi$, on peut réfuter l’existence d’une trajectoire fermée pour le système original.
Théorème de Dulac.Considérez les mêmes hypothèses que pour le théorème de Bendixson. De plus, supposons que l’on puisse trouver une fonction continûment différentiable $\varphi :\mathbb{R}^2\to\mathbb{R}$.telle que$$ \frac{\partial (\varphi f)}{\partial x}(x,y)+\frac{\partial (\varphi g)}{\partial y}(x,y) $$
n’est pas identiquement nulle (c’est-à-dire, non nulle pour tout $(x,y)$ dans $D$) et a un signe donné dans $D$, alors il n’y a pas de cycles dans $D$.
La fonction $\varphi$ est généralement appelée fonction de Dulac. Malheureusement, il n’existe pas d’algorithme pour trouver de telles fonctions. Appliquons le théorème de Dulac dans deux exemples précédemment étudiés pour lesquels nous avons observé l’absence de cycles.
Plus de requins et de sardines. Voici le système
$$ \begin{cases} \dot{x}= x\, (1-x-y)\\ \dot{y}= \beta\, (x-\alpha)y \end{cases} $$
où $\alpha,\beta>0$.
Rappelons que nous étudions ce système à l’intérieur du quadrant positif.
Soit
$$ \varphi(x,y)=\frac{1}{xy} $$
qui est bien défini pour $x,y>0$. Nous avons
$$ \frac{\partial (\varphi f)}{\partial x}(x,y)+\frac{\partial (\varphi g)}{\partial y}(x,y)=-\frac{1}{y}\cdot $$
Ceci est strictement négatif, donc il ne peut y avoir de cycles dans ce modèle.
Retour à notre modèle de deux populations en compétition. Nous avons les équations
$$ \begin{cases} \dot{x}= x\, (1-x-a_{12}y)\\ \dot{y}= \rho y\, (1-y-a_{21}x) \end{cases} $$
où $\rho,a_{12},a_{21}>0$. Encore une fois, nous ne considérons que le premier quadrant, et nous utilisons la même fonction de Dulac que précédemment. Nous obtenons
$$ \frac{\partial (\varphi f)}{\partial x}(x,y)+\frac{\partial (\varphi g)}{\partial y}(x,y)=-\left(\frac{1}{y}+\frac{\rho}{x}\right)\cdot $$
Puisque nous une quantité strictement négative pour tout $x,y>0$, il n’y a pas de cycle dans ce modèle.

